I stumbled across an interesting RPG called Kapow! that features a dice mechanic I've not seen before: powers are assigned 2 dice, like d10, d10, or d8, d6. You don't add the dice together, though: you roll both and take the higher of the two results. Not having a good head for probabilities and stats, I'm wondering if someone could explain how that affects outcomes. For example, when you roll d8 twice and take the higher result, does that change the average roll result? How much of the time will d8, d8 beat d8, d6?
j8cob The Gr8est / The J8est
Member
Seen
11 days ago
So the probability to roll any given number on a d6 would be .16 repeating, so we can round up to .17. The probability of rolling any number on a d8 would be .125, which for simplicity we'll round up to .13. In order to get a number equal to or higher than a 6 on a d8 it would be about a .38 chance. Basically 6 in 10 rolls on a d8 will be within the value of a d6, but 4 in 10 rolls will be higher.
Now the part we don't need any math for: there is a .0 chance of a d6 rolling higher than a 6. If you want the highest numbers possible then choosing a smaller die will fail you. Not only are the individual odds of rolling a number available on a d6 smaller on a d8 but the d8 has a higher maximum than the d6. There is no real benefit to rolling two die of different values other than for novelty or to abide by a rule, unless you want smaller numbers intentionally.
Now the part we don't need any math for: there is a .0 chance of a d6 rolling higher than a 6. If you want the highest numbers possible then choosing a smaller die will fail you. Not only are the individual odds of rolling a number available on a d6 smaller on a d8 but the d8 has a higher maximum than the d6. There is no real benefit to rolling two die of different values other than for novelty or to abide by a rule, unless you want smaller numbers intentionally.
OP
Clever Hans Hoof-based mathematician
Member
Seen
2 yrs ago
[Gears in brain grinding slowly]
The game system has different power levels. Level 7, for example, is d8, d6. Level 8 is d8, d8. As you surmsied, the intent is indeed for smaller results to come from lower power levels.
Does rolling two of the same die and taking the higher result actually give you better odds of producing a higher result? This is what's really making my head spin.
The game system has different power levels. Level 7, for example, is d8, d6. Level 8 is d8, d8. As you surmsied, the intent is indeed for smaller results to come from lower power levels.
Does rolling two of the same die and taking the higher result actually give you better odds of producing a higher result? This is what's really making my head spin.
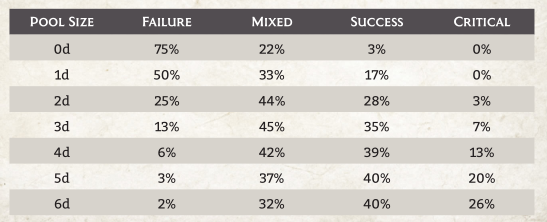
I am no mathematician but this is relevant to a rp I'm DMing at the moment. We use D6s only though. 3d6 in a stat means it's your best stat, 2d6 means your pretty competent. In this system a 6 is a success, a 4 or 5 is a Mixed Success, a 1 to 3 is a failure and two 6's are a critical success.
Here are the percentage chance of rolling something on a D6 system:
I'd be really curious to see how much % chance switching from a D6 to a D8 actually affects your chances though. Now you've got me looking up the system...
Here are the percentage chance of rolling something on a D6 system:

I'd be really curious to see how much % chance switching from a D6 to a D8 actually affects your chances though. Now you've got me looking up the system...
BrokenPromise With Rightious Hands
Member
Seen
7 hrs ago
Does rolling two of the same die and taking the higher result actually give you better odds of producing a higher result? This is what's really making my head spin.
Short answer: Rolling multiple die and taking the better result not only more frequently yields a higher result, it more consistently avoids lower rolls.
In the game you describe, you roll 2 dice, and you always take the die with the better result. If you were just rolling 1, you have a 1-out-of-6 chance to get a 6. This is easy to see, because all we need to do is count the number of sides on the dice, which will give us all our possible outcomes.
1,2,3,4,5,6
It gets trickier for two dice. Because to find every possible combination, we need to multiply this by the number of sides for each additional dice. 6 X 6 = 36, and all the combinations are as follows:
1/1,1/2,1/3,1/4,1/5,1/6,
2/1,2/2,2/3,2/4,2/5,2/6,
3/1,3/2,3/3,3/4,3/5,3/6,
4/1,4/2,4/3,4/4,4/5,4/6,
5/1,5/2,5/3,5/4,5/5,5/6,
6/1,6/2,6/3,6/4,6/5,6/6,
See? 36. If we rolled 3 6 sided die, we'd have 6 X 6 X 6 = 216 possible combinations. But we won't worry about that for now.
So going back to our possible outcomes for a single die, you can see that there's a 1-in-6 chance of getting a 1 or a 6. But when using 2 dice, it's clear things aren't quite so balanced. Statistically speaking, you have a 1-in-36 chance to get a 1 and a gnarly 11-in-36 chance to get a 6. Had you been rolling a single die, you'd roll a 6 6 times, almost half as frequently. And you'd have rolled 5 more 1s.
EDIT: should probably mention that the number of outcomes does not always equal the percent chance of getting a particular outcome. But in this case where all the dice have the same number of sides, each dice has the same % chance to land on any particular side.
2x Thank


BrokenPromise With Rightious Hands
Member
Seen
7 hrs ago
I'd be really curious to see how much % chance switching from a D6 to a D8 actually affects your chances though. Now you've got me looking up the system...
The chance of landing on any side of an 8-sided dice is 12.5%. Therefor, you have a 25% chance of rolling something that is unattainable on a 6-sided dice, and a 37.5% chance to at least get something equal to the highest number on a 6. Compare that to a 0% or 16%-ish chance respectively. Or if you prefer a non % based representation of this in the real world, let's do number of times out of 24 since that's a number both 6 and 8 go into. If you rolled both dice 24 times, the d6 would give you a 6 only 4 times, where the d8 would give you a 6 or greater an astounding 9 times.
Another fun test, let's pretend you have "perfectly normal" luck and you'll always roll each side of the dice the same number of times. in 24 rolls, You'd roll every side of the d6 4 times which is (1 + 2 + 3 + 4 + 5 + 6) X 4 = 84. Meanwhile, with the 8 you would get each side 3 times for a total of (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8) X 3 = 108
@BrokenPromise that's so cool. Thankyou for taking the time to explain the math behind it. I think I understand the difference way better now, and it's quite a significant change!
1x Like


OP
Clever Hans Hoof-based mathematician
Member
Seen
2 yrs ago
<Snipped quote by Mae>
The chance of landing on any side of an 8-sided dice is 12.5%. Therefor, you have a 25% chance of rolling something that is unattainable on a 6-sided dice, and a 37.5% chance to at least get something equal to the highest number on a 6. Compare that to a 0% or 16%-ish chance respectively. Or if you prefer a non % based representation of this in the real world, let's do number of times out of 24 since that's a number both 6 and 8 go into. If you rolled both dice 24 times, the d6 would give you a 6 only 4 times, where the d8 would give you a 6 or greater an astounding 9 times.
Another fun test, let's pretend you have "perfectly normal" luck and you'll always roll each side of the dice the same number of times. in 24 rolls, You'd roll every side of the d6 4 times which is (1 + 2 + 3 + 4 + 5 + 6) X 4 = 84. Meanwhile, with the 8 you would get each side 3 times for a total of (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8) X 3 = 108
One more question, if I may: In a contested roll, you have d8, d8. I have d8, d6. What's the percentage chance that you will roll higher? What's the chance that I roll higher?
BrokenPromise With Rightious Hands
Member
Seen
7 hrs ago
@Clever Hans You'd better not be trying to get me to do your math homework.
For simplicity, let's work on one set of dice at a time. Your d8 VS my d8.
We both have the same chance of landing on any particular side. Both of our die have 8 sides, so there are 8 X 8 = 64 different scenarios that all have the exact same chance of occurring.
If I roll an 8, I'll have beaten 7 out of 8 possible outcomes you could roll. 7 beats 6, 6 beats 5, until I roll a 1 which can't beat anything. So we just have to add all my victories together and compare them to the number 64 to see my chances.
7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 = 28
We both have a 28/64 chance of winning, or 43.75%. The remaining 8 rolls we tied (12.50%) We'll keep this in mind for later.
I don't think it's going to matter too much that a d6 has a slightly higher chance of landing on all of its sides. It has a better chance of landing on smaller numbers and higher numbers. Moreover, 16.6666666...% repeating is hard to do math stuff with compared to the totally chill 12.5% offered by a d8. Regardless, all outcomes should more or less have the same chance of happening, which is what matters.
Same as before, we multiply the sides of our dice together.
6 X 8 = 48
This time you have a d6. That means that for each side of my die, there's 6 possible outcomes. If I roll a 7 or an 8, I win every time. Then from 6 and below it becomes possible for me to lose. So we can add that up like so:
6 + 6 + 5 + 4 + 3 + 2 + 1 + 0 = 27
And for you it's pretty much the exact opposite:
0 + 0 + 0 + 1 + 2 + 3 + 4 + 5 = 15
And then we tie on 6 rolls, which should account for our 48 rolls.
27/48 = 56.25% = my chance of winning
15/48 = 31.25% = your chance of winning
6/48 = 12.5% = the chance we tie
Now
We now know each dice's chances of beating another dice. But it gets a little interesting here because we aren't rolling these dice as sets. We're rolling both our dice at the same time and seeing who has the highest number. As an example, my first d8 might have been a 5, which was higher than the 4 you rolled, but you rolled a 6 on your d6 and my other die was a 1. So you would have won that. But at any given time, I'm only going to have one die that has my highest number, or two dice with an equal number. Ultimately, any of my dice has to compete with any of your dice. so the outcomes are:
My first d8 against your d8
My second d8 against your d8
My first d8 against your d6
My second d8 against your d6
Because there are so many d8s, this wasn't even really worth considering, since 50% of the contests are going to be like one of the two scenarios mentioned above. So that makes this part pretty simple. We're going to divide our %s in half and add them together. And in the end...
I have a (43.75% + 56.25%) ÷ 2 = 50.00% chance to win.
You have a (43.75% + 31.25%) ÷ 2 = 37.50% chance to win.
And we have a 12.5% chance to tie.
For simplicity, let's work on one set of dice at a time. Your d8 VS my d8.
We both have the same chance of landing on any particular side. Both of our die have 8 sides, so there are 8 X 8 = 64 different scenarios that all have the exact same chance of occurring.
If I roll an 8, I'll have beaten 7 out of 8 possible outcomes you could roll. 7 beats 6, 6 beats 5, until I roll a 1 which can't beat anything. So we just have to add all my victories together and compare them to the number 64 to see my chances.
7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 = 28
We both have a 28/64 chance of winning, or 43.75%. The remaining 8 rolls we tied (12.50%) We'll keep this in mind for later.
I don't think it's going to matter too much that a d6 has a slightly higher chance of landing on all of its sides. It has a better chance of landing on smaller numbers and higher numbers. Moreover, 16.6666666...% repeating is hard to do math stuff with compared to the totally chill 12.5% offered by a d8. Regardless, all outcomes should more or less have the same chance of happening, which is what matters.
Same as before, we multiply the sides of our dice together.
6 X 8 = 48
This time you have a d6. That means that for each side of my die, there's 6 possible outcomes. If I roll a 7 or an 8, I win every time. Then from 6 and below it becomes possible for me to lose. So we can add that up like so:
6 + 6 + 5 + 4 + 3 + 2 + 1 + 0 = 27
And for you it's pretty much the exact opposite:
0 + 0 + 0 + 1 + 2 + 3 + 4 + 5 = 15
And then we tie on 6 rolls, which should account for our 48 rolls.
27/48 = 56.25% = my chance of winning
15/48 = 31.25% = your chance of winning
6/48 = 12.5% = the chance we tie
Now
We now know each dice's chances of beating another dice. But it gets a little interesting here because we aren't rolling these dice as sets. We're rolling both our dice at the same time and seeing who has the highest number. As an example, my first d8 might have been a 5, which was higher than the 4 you rolled, but you rolled a 6 on your d6 and my other die was a 1. So you would have won that. But at any given time, I'm only going to have one die that has my highest number, or two dice with an equal number. Ultimately, any of my dice has to compete with any of your dice. so the outcomes are:
My first d8 against your d8
My second d8 against your d8
My first d8 against your d6
My second d8 against your d6
Because there are so many d8s, this wasn't even really worth considering, since 50% of the contests are going to be like one of the two scenarios mentioned above. So that makes this part pretty simple. We're going to divide our %s in half and add them together. And in the end...
I have a (43.75% + 56.25%) ÷ 2 = 50.00% chance to win.
You have a (43.75% + 31.25%) ÷ 2 = 37.50% chance to win.
And we have a 12.5% chance to tie.
2x Like


OP
Clever Hans Hoof-based mathematician
Member
Seen
2 yrs ago
@Clever Hans You'd better not be trying to get me to do your math homework.
<lots of amazingness edited out>
I have a (43.75% + 56.25%) ÷ 2 = 50.00% chance to win.
You have a (43.75% + 31.25%) ÷ 2 = 37.50% chance to win.
And we have a 12.5% chance to tie.
Hah! No homework, I swear. Just trying to wrap my head around an interesting but perplexing resolution system. That was really awesome. Thank you so very much!
Now, what happens if one person is d8, d8, and the other is d10, d8?
I keed, I keed! Don't maim me! :D
© 2007-2024